Zero-Knowledge Proof Reconstruction for Graph 3-Colourability

💡Project Website: https://fellahi.ca/zk-proof-demo/
💡GitHub Repository: https://github.com/nouhailafellahi/zk-proof-demo
In what kinds of scenarios could one come face to face with a wild zero-kowledge proof? #
Zero-knowledge proofs emerged from the need to convey characteristics of pieces of information without revealing said information.
For example, convincing a friend that you know their birthday without revealing the date to the friends around you.
A more realistic use for zero-knowledge proofs would be in B2B interactions: Retail company A wants to buy a large dataset of sample customer information from company B in order to better train their AI recommendation algorithm. Company A, however, wants to be certain that the data set meets certain quality standards before buying it.
This can’t be done by letting company A review the dataset to confirm its quality because then they would already have possession of the dataset and would have no incentive to buy/pay for it. A solution to this problem is the use of zero-knowledge proofs.
Through the encryption of the dataset and a back and forth between company A and B using said encrypted set , company A can be convinced of the quality of the product company B is selling to them without jeopardizing company B!
Interactive Zero-Knowledge Proofs #
The specific type of proof used in our subject application is called Interactive Zero-Knowledge Proof. They involve multiple rounds of interactions between the prover and verifier. During each round, the verifier subjects the prover to multiple challenges that reinforce the validity of the prover’s claims if answered right, and invalidate their claims if not. This interchange can be repeated as many times as the verifier needs to feel convinced in the soundness of the prover’s claims.
(For reference, in the scenario introduced in the previous paragraph, company A would be the verifier and company B would be the prover. While suitable quality of the subject dataset would be the prover’s (company B) claim that would be assessed by the verifier (company A))
Zero-Knowledge Protocol for Graph 3-Colourings #
Remember how we said that interactive zero-knowledge proofs consist of rounds of challenges posed by the verifier and answered by the prover? Let’s see what a round of challenges and answers looks like in order to formulate a zero-knowledge proof for 3-colourable graphs.
Let $G$ be a graph on $n$ number of vertices. Let the set of vertices be
$V = {v_1, …, v_n}$
and the set of edges be
$E = {e_{i,j} : ∃ \ edge \ between \ v_i, v_j }$
At the beginning both the prover (P) and verifier (V) know the graph $G$. The prover (P) has additional, private information: a 3-colouring $w$ of the graph, possibly valid. (Reminder: a valid 3-colouring means that each vertex of the graph G is assigned one of three colours such that no two adjacent vertices share the same colour.)
Prover: given $w$, randomly permute the assignment of the three colours to obtain a new colouring. (This change maintains the validity of the colouring. If the colouring is a valid 3-colouring, it remains so after the colour permutation. If the colouring is not a valid 3-colouring, it remains so after the colour permutation.) Then use a commitment scheme to commit all the colours to their respective vertices. (A commitment scheme cryptographically assures that the prover is not able to tamper with the chosen colouring of the graph once it is committed)
$∀i ∈ [n], c_i = COM(v_i, colour \ of \ v_i)$
For each vertex $v_i$ in the set of vertices $V$, the prover creates a commitment $c_i$ to the chosen colour of $v_i$. Here, $COM$ denotes the commitment function.
Verifier: select an edge $e_{i,j}$ from the set of edges $E$ and send $e_{i,j}$ to the prover. This step is random, meaning that the verifier can pick any edge they would like.
Prover: Open the commitments $c_i$ and $c_j$corresponding to the vertices of the edge $e_{i,j}$. This means that the prover reveals the colours of $v_i$ and $v_j$.
Verifier: Check the colours of $v_i$ and $v_j$ and
-
Accept if the colour of $v_i$ ≠ $v_j$. (The colours of the vertices for the chosen edge are different)
-
Decline if the colour of $v_i$ = $v_j$. (The colours of the vertices for the chosen edge are the same, proving that the colouring the prover has is not a valid 3-colouring)
This protocol allows:
- The prover to convince the verifier they have a valid 3-colouring without revealing the entire colouring.
- The verifier to be confident in the proof as the commitment scheme ensures that the prover cannot change the colour once it has been committed, guaranteeing the integrity of the proof.
- The verifier to probabilistically check the validity of the 3-colouring by continuously choosing random edges during each round of the proof.
How is the presented application a reconstruction of interactive zero-knowledge proof? #
Let’s understand how it all fits into the scope of the application.
Let’s set up the stage first:
- Verifier: you
- Prover: Application
- Information to be verified: the existence of a 3-colour scheme for the chosen graph. (i.e. the ability to colour the graph’s nodes using three colours such that no two neighboring nodes are of the same colour)
Note: the prover hides the colouring from the verifier the entire duration of the two following steps.
- Prover: Shuffles the graph colouring (changing the colouring scheme or choosing a different colouring permutation).
- Prover: Assigns and commits to each node the appropriate colour. Once it is committed, it’s impossible to tamper with the chosen colouring.
- Prover: Presents the verifier with the graph.
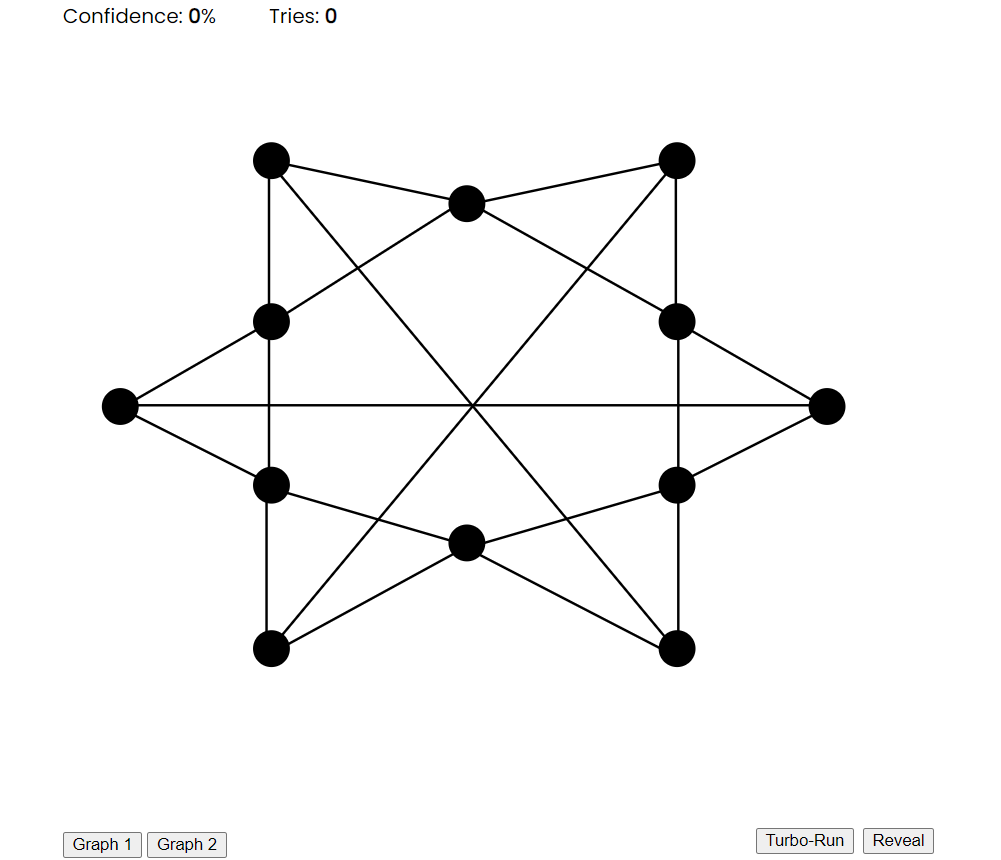
- Verifier: Picks an edge of their choosing.
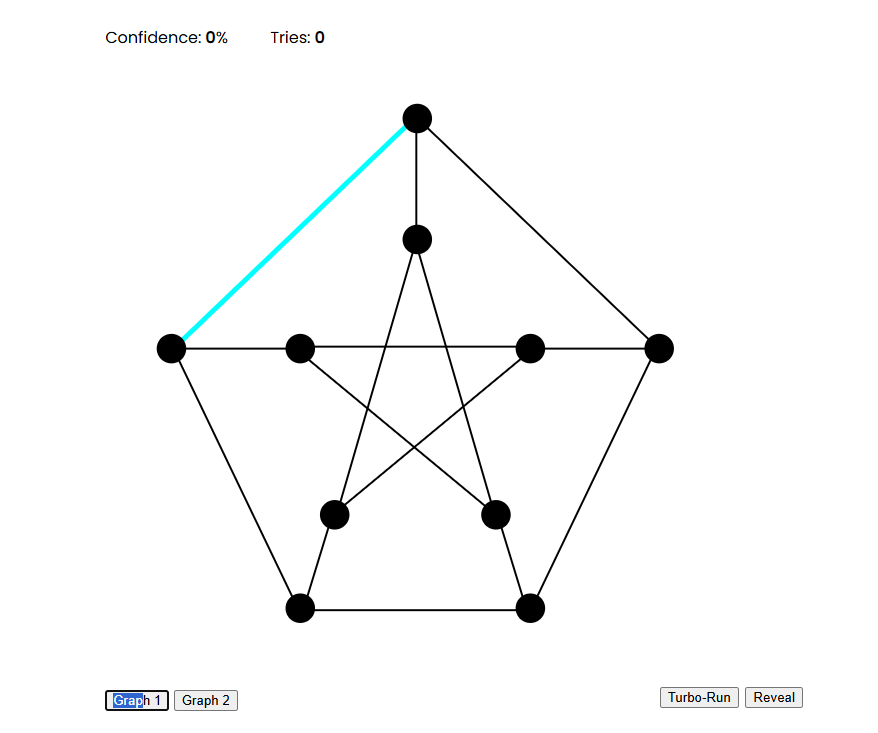
- Prover: Reveals the colouring of the two end-point nodes for the chosen edge in front of the verifier.
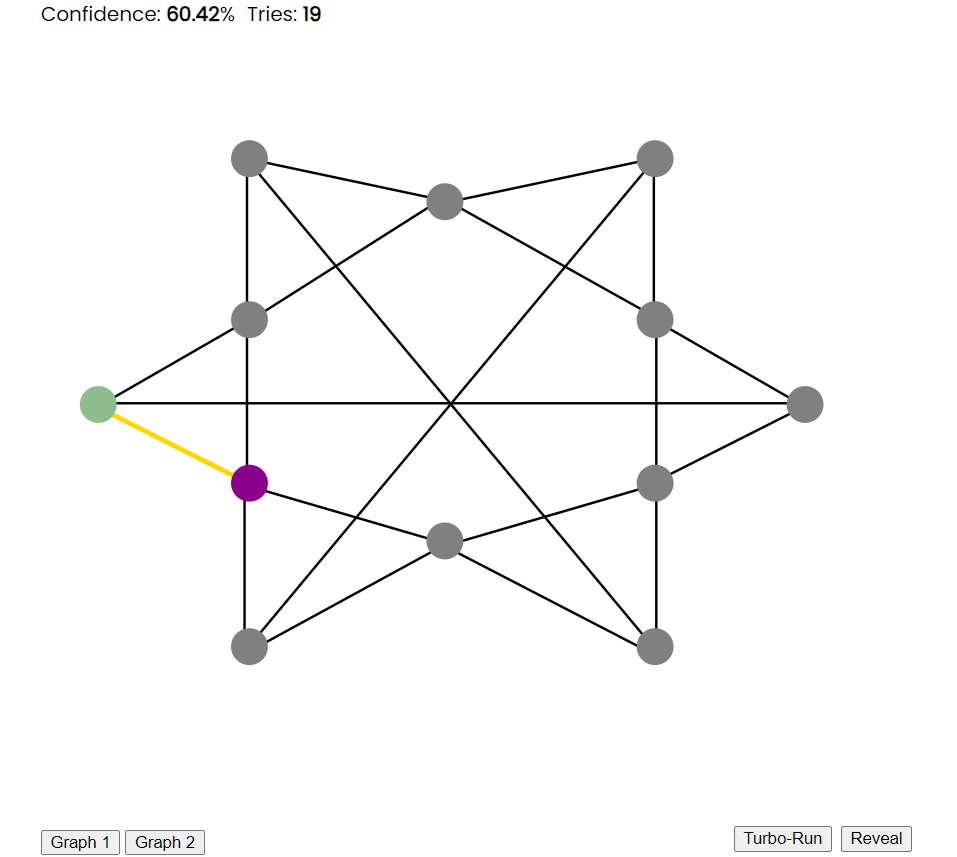
- Verifier: If the colours of the two nodes are the same, then the verifier is 100% certain that the prover does not possess a valid 3-colour scheme for the subject graph and the proving process is over. If the colours of the two nodes are different, however, the verifier is a little more certain that the prover has a valid 3-colour scheme for the subject graph. (The certainty in the prover at each repetition of these steps is represented using the Confidence value at the top of the graph).
Option 1: differently coloured nodes.
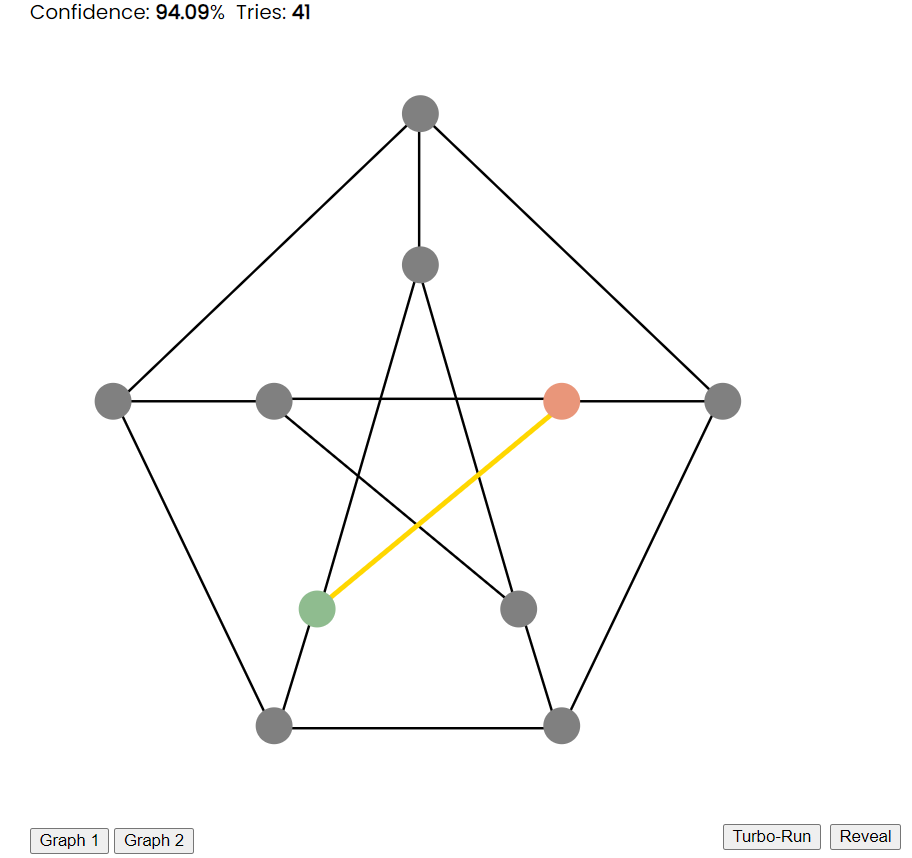
Option 2: similarly coloured nodes.
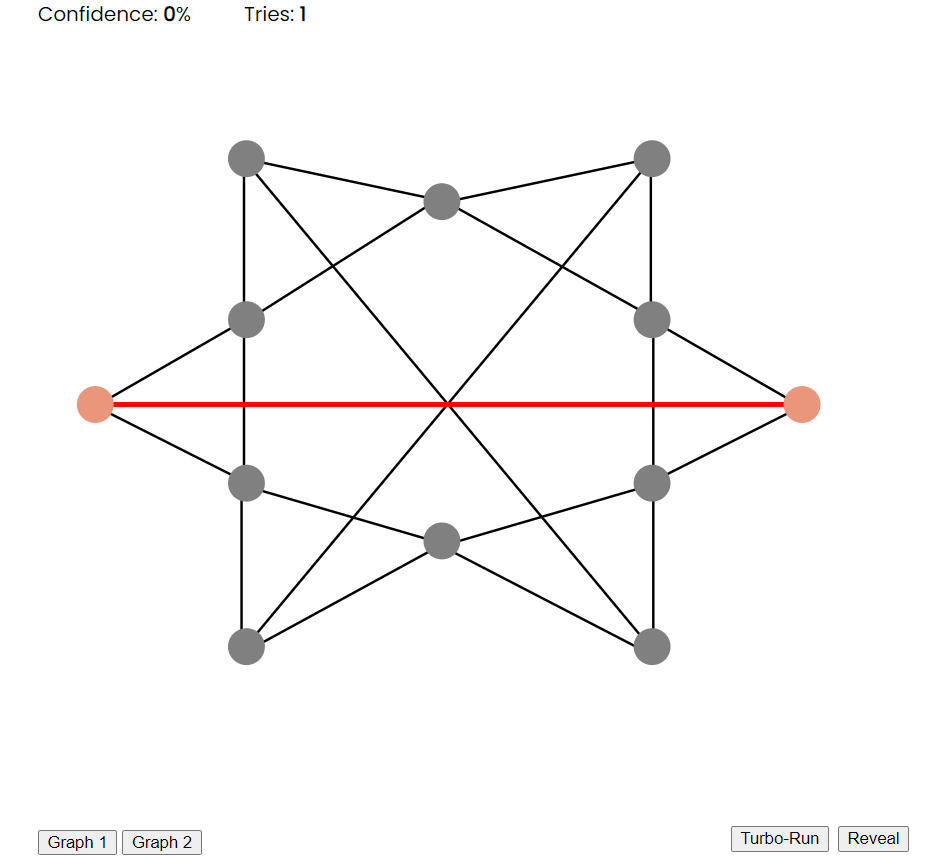
In this way the verifier will never be able to figure out the colourings that the prover possesses while being able to achieve an infinitely high level of confidence in the prover’s claims.
To conclude #
The proof hinges on the idea that the more repetitions happen without finding similarly coloured nodes, the less likely it is to eventually find two nodes of the same colour (which would invalidate the proof). So the higher the confidence rises, the more willing the verifier is to bet on the assumption that the prover is honest.